分析、统计算法的执行效率和资源消耗

1. 大 O 复杂度表示法
算法的执行效率简单来说,就是算法代码执行的时间。
例如下面这段代码:
int cal(int n) {
int sum = 0; // 1
int i = 1; // 1
for (; i <= n; ++i) { // n
sum = sum + i; // n
}
return sum;
}
每一行都执行着类似的操作:读数据-运算-写数据。
假设每行代码执行的时间都相同,为unit_time。则第 2、3 行代码分别需要 1 个unit_time的执行时间。第 4、5 行都运行了 n 遍,所以需要2n * unit_time的执行时间。所以总的执行时间就是(2n+2) * unit_time。
对于下面这段代码:
int cal(int n) {
int sum = 0; // 1
int i = 1; // 1
int j = 1; // 1
for (; i <= n; ++i) { // n
j = 1; // n
for (; j <= n; ++j) { // n^2
sum = sum + i * j; // n^2
}
}
}
整段代码的执行时间为T(n) = (2n^2 + 2n + 3) * unit_time。
可以看到,所有代码的执行时间
T(n)与每行代码的执行次数成正比。
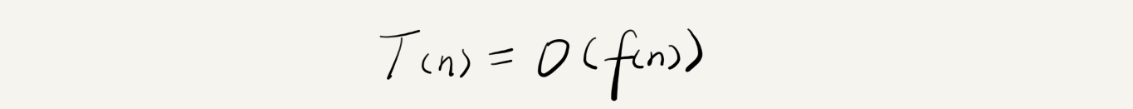
其中,
T(n):表示代码的执行时间n:表示数据规模的大小f(n):表示每行代码执行的次数总和O:表示代码的执行时间T(n)与f(n)表达式成正比
大 O 时间复杂度实际上并不具体表示代码真正的执行时间,而是表示代码执行时间随数据规模增长的变化趋势,所以也叫做渐进时间复杂度 (Asymptotic Time Complexity),简称时间复杂度。
用大 O 表示法表示刚才两段代码的时间复杂度,分别为
T(n)=O(n)、T(n)=O(n^2)
2. 时间复杂度分析
- 只关注循环执行次数最多的一段代码
- 加法法则:总复杂度等于量级最大的那段代码的复杂度
- 乘法法则:嵌套代码的复杂度等于嵌套内外代码复杂度的乘积
3. 几种常见的时间复杂度

3.1 非多项式时间复杂度
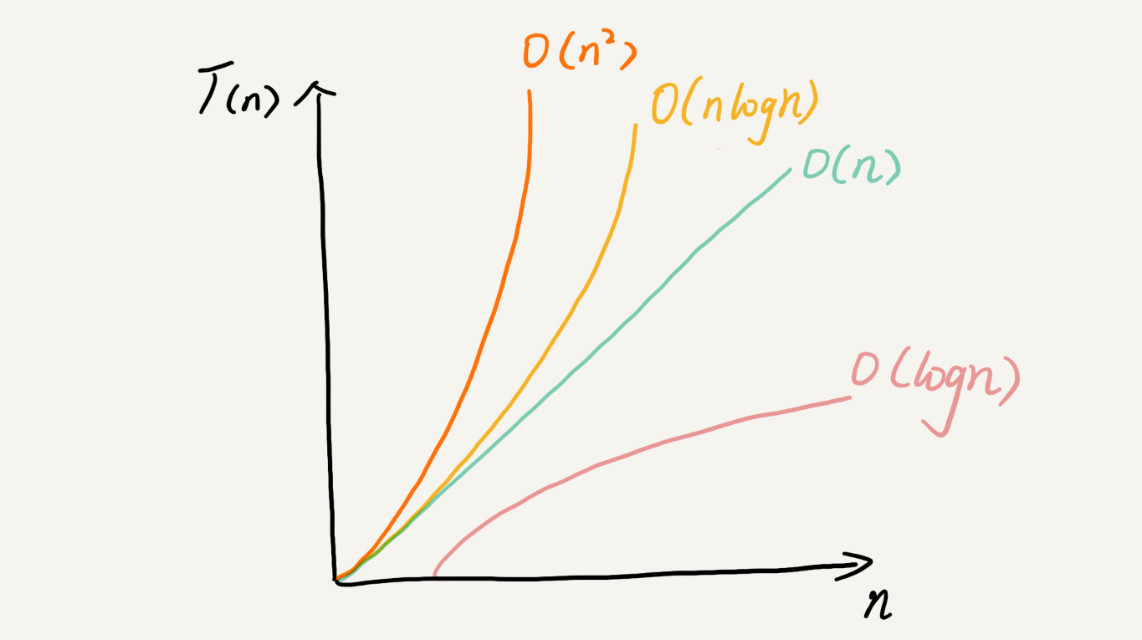
可以将上图中的复杂度量级粗略分为两类:多项式量级和非多项式量级。其中,非多项式量级只有两个:O(2^n)和O(n!)。
当数据规模n越来越大时,非多项式量级算法的执行时间会急剧增加,求解问题的执行时间会无限增长。所以,非多项式时间复杂度的算法其实是非常低效的算法。
3.2 多项式时间复杂度
1. O(1)
只要代码的执行时间不随n的增大而增长,这样代码的时间复杂度都记作O(1)。
int i = 8;
int j = 6;
int sum = i + j;
一般情况下,只要算法中不存在循环、递归语句,即使有成千上万行的代码,其时间复杂度也还是
O(1)
2. O(logn)、O(nlogn)
对数阶时间复杂度非常常见,同时也最难分析。例如下面的代码:
i=1;
while (i <= n) {
i = i * 2;
}
实际上,变量i的取值就是一个等比数列:

可得x=log_2^n。忽略对数的底,统一表示为O(logn)。
根据前面提到的乘法法则,如果一段代码的时间复杂度是O(logn),循环执行n遍,时间复杂度就是O(nlogn)了。
O(nlogn)也是一种非常常见的算法时间复杂度,例如归并排序、快速排序的时间复杂度都是O(nlogn)
3. O(m+n)、O(m*n)
有时代码的复杂度由两个数据的规模来决定:
int cal(int m, int n) {
int sum_1 = 0;
int i = 1;
for (; i < m; ++i) {
sum_1 = sum_1 + i;
}
int sum_2 = 0;
int j = 1;
for (; j < n; ++j) {
sum_2 = sum_2 + j;
}
return sum_1 + sum_2;
}
从代码中可以看出,m和n分别表示两个数据规模,我们无法事先评估m和n谁的量级更大。因此不能简单的利用加法法则,而要将时间复杂度表示为O(m+n)。
这种情况下加法法则需要改为:T1(m) + T2(n) = O(f(m) + g(n))。
而乘法法则继续有效:T1(m) * T2(n) = O(f(m) * f(n))。
4. 空间复杂度分析
类比时间复杂度,空间复杂度的全称就是渐进空间复杂度 (Asymptotic Space Complexity),表示算法的存储空间与数据规模之间的增长关系。
常见的空间复杂度就是
O(1)、O(n)、O(n^2),像O(logn)、O(nlogn)这样的对数阶复杂度平时基本用不到
5. 复杂度小结
- 复杂度也叫渐进复杂度,包括时间复杂度和空间复杂度,用来分析算法执行效率与数据规模之间的增长关系
- 越高阶复杂度的算法,执行效率越低
- 常见的复杂度并不多,从低阶到高阶有:
O(1)、O(logn)、O(n)、O(nlogn)、O(n^2)
