最好情况、最坏情况、平均情况、均摊时间复杂度

继续来看四个复杂度分析方面的知识点:最好情况时间复杂度 (Best Case Time Complexity)、最坏情况时间复杂度 (Worst Case Time Complexity)、平均情况时间复杂度 (Average Case Time Complexity)、均摊时间复杂度 (Amortized Time Complexity)。
1. 最好、最坏情况时间复杂度
例如在一个无序数组array中查找变量x出现的位置:
// n 表示数组 array 的长度
int find(int[] array, int n, int x) {
int i = 0;
int pos = -1;
for (; i < n; ++i) {
if (array[i] == x) {
pos = i;
break;
}
}
return pos;
}
- 最好情况时间复杂度:在最理想的情况下,执行这段代码的时间复杂度,这里为
O(1) - 最坏情况时间复杂度:在最糟糕的情况下,执行这段代码的时间复杂度,这里为
O(n)
2. 平均情况时间复杂度
还是上面的例子:要查找变量x在数组中的位置,有n+1种情况:在数组的0 ~ n-1位置中和不在数组中。我们把每种情况下,查找需要遍历的元素个数累加起来,然后再除以n+1,就可以得到需要遍历的元素个数的平均值,即:
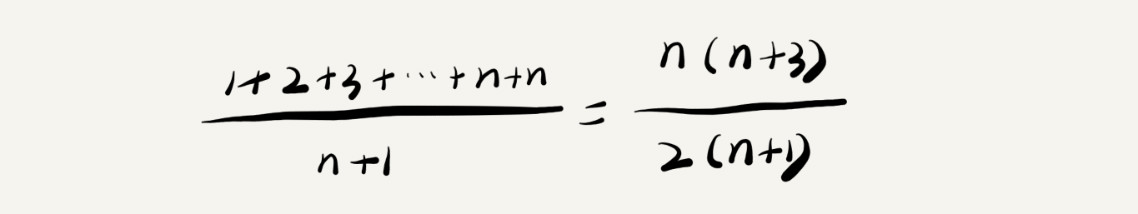
简化后得到的平均时间复杂度为O(n)。
然而上面的考虑还不够全面:若假设变量x在数组中与不在数组中的概率都为1/2,则可得加权平均时间复杂度或者期望时间复杂度:
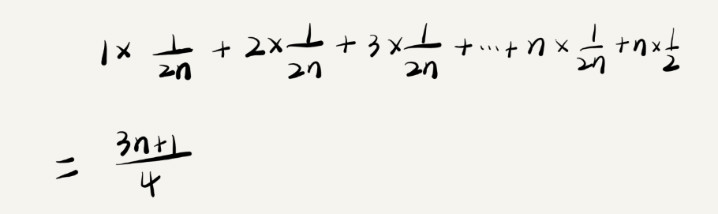
去掉系数和常量,这段代码的加权平均时间复杂度仍为O(n)。
3. 均摊时间复杂度
大部分情况下,我们并不需要区分最好、最坏、平均三种复杂度。平均复杂度只在某些特殊情况下才会用到,而均摊时间复杂度应用的场景比它更加特殊、更加有限。
// array 表示一个长度为 n 的数组
// 代码中的 array.length 就等于 n
int[] array = new int[n];
int count = 0;
void insert(int val) {
if (count == array.length) {
int sum = 0;
for (int i = 0; i < array.length; ++i) {
sum = sum + array[i];
}
array[0] = sum;
count = 1;
}
array[count] = val;
++count;
}
这段代码实现了一个往数组中插入数据的功能。当数组满了之后,用for循环遍历数组求和,并清空数组,将求和之后的sum值放到数组的第一个位置,然后再将新的数据插入。但如果数组一开始就有空间空间,则直接将数据插入数组。
- 最好情况:
O(1) - 最坏情况:
O(n) - 平均复杂度:
O(1)
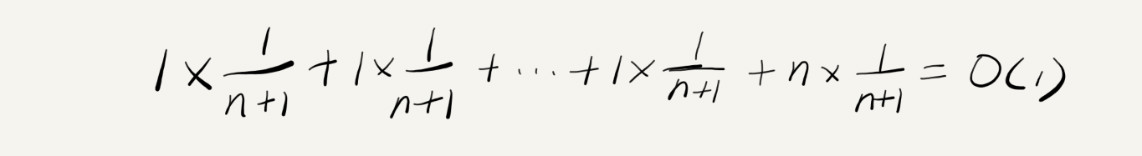
还是insert()函数这个例子:随着n的不断增长,可以发现每一次O(n)的插入操作,都会跟着n-1次O(1)的插入操作。所以把耗时多的那次操作均摊到接下来的n-1次耗时少的操作上,这一组连续的操作的均摊时间复杂度就是O(1)。这就是均摊分析(又称摊还分析)的大致思路。
简单来看,均摊时间复杂度就是一种特殊的平均时间复杂度
